How to calculate the volume of a cone
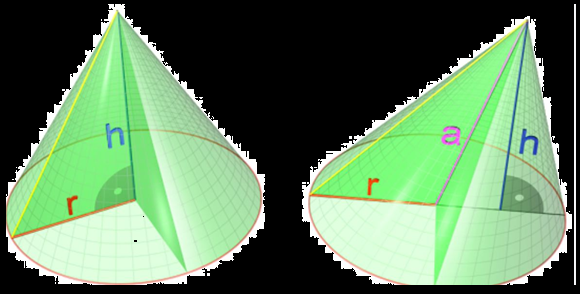
A closed three-dimensional geometric shape, consisting of two sides of a right-angled triangle and a circular curve is called a cone, and it results from the rotation of the right-angled triangle with a full 360° angle, around one of its right-angled sides. (as shown in the fig)
Properties of a Cone
The guideline is the circular curve of the cone.
The vertex of the cone is the point between the other two sides of the triangle, and a certain distance from the circular base of the cone.
The connecting line in a cone is the straight lines drawn from the vertex of the cone to its base.
When the connecting lines are unequal in length is called a circular cone.
A cone is of the right circular type when all the lines joining the graph are equal in length.
The area of a cone
= Sum of its lateral area and the Area of a circle or base.
The volume of a cone
= (height x π x radius squared) ÷ 3
How to calculate the volume of a cone
How to calculate the volume of a cone
We can calculate the volume of the cone by knowing the height “h” and the length of the radius of the circle at its base “r”,
where the volume of the cone is equal to one-third of the product of the base area x height, and this relationship can be expressed through the following formula:
The volume of the cone = (height × π × radius squared) ÷ 3,
Note: the symbol π is a Greek symbol called “pi”, which has a constant value of 22/7 or 3.14,
And units are cubic units
Examples:
Calculate the area of a cone whose base length is 8 cm and height is 3 cm, given that π = 22/7.
Solution:
Volume of the cone
= (height × π × radius squared) ÷ 3
Radius = 8 ÷ 2 = 4 cm.
Volume of the cone
= (4² x 3 x 2/7) ÷ 3
= 50.24 cubic centimeters
Area of cone
The area of a cone is divided into two parts, as it results from the sum of the lateral area of the cone with the area of the base, and can be expressed as:
Total area (T) = Area of the base + Curved Surface area
Since the base is a circle, the area of the base = πr2
T = πr2 + πrl
T = πr(r + l)
Where l is the length of the cone's line.
Calculate the area of the base of the cone
The area of the base of the cone can be calculated using the formula of the area of a circle, which is the product of the value of “l”, multiplied by the square of the length of the radius of the circle.
Calculate the lateral area of a cone
We can calculate the area of the lateral sector of a cone by multiplying the area of the circle x dividing the measure of the central angle by 360 degrees,
Knowing that the measure of the central angle is 180 degrees, and this relationship can be expressed as
“Area of the circular sector = (measure of the central angle of the circular sector ÷ 360°) × area of the circle”.
Examples of the area of a cone
Solid cone, with a diameter of 3 cm, calculate its lateral area.
Given: Diameter = 3 cm,
Radius r = Diameter ÷ 2 = 1.5 cm,
π = 22/7.
Solution:
The lateral area of the cone
= (measure of the central angle ÷ 360) x the area of the circular base.
The lateral area of the cone = (180 ÷ 360) × π × r².
The lateral area of the cone = 1/2 x 22/7 x 1.5²
The lateral area of the cone = 3.5 square centimeters.
Read Also






0 Comments